9-сынып: геометриялық прогрессияның алғашқы n мүшелерінің қосындысының формуласы
Жаңатаң орта мектебі
Бекітемін:
Оқу ісінің орынбасары А. Ж. Тулеуова
Ашық сабақ
Тақырыбы:
«Геометриялық прогрессияның алғашқы n - ші мүшесінің формуласы»
9 класс
Өткізген: математика пәнінің мұғалімі Қыйлыбаева Ақгүл Орынбекқызы
2014 - 2015 оқу жылы
Сабақтың мақсаты: Геометриялық прогрессияның алғашқы n - ші мүшесінің қосындысының формуласын меңгеріп, есептер шығаруға қолдана білу.
Сабақтың типі: жаңа сабақ
Сабақтың көрнекілігі: интерактивті тақта, кеспе қағаздар, деңгейлік тапсырмалар
Сабақтың барысы:
І. Ұйымдастыру:
- Оқушылармен амандасу;
- Сабаққа қатысымын тексеру, назарын сабаққа аудару;
- Сабақтың тақырыбын, мақсатын хабарлау.
ІІ. Психологиялық тренинг: «Мен саған сенемін . . . »
Жұп құрып, бір - бірінің көздеріне қарап отырыңыздар.
«Мен саған сенемін, өйткені …. . »
деп жалғастырасыздар.
Мысалы: «Мен саған сенемін, өйткені сен жақсы адамсың»
ІІІ. Өткенді қайталау.
Геометриялық прогрессияның
n мүшесінің формуласы.
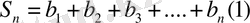
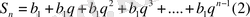
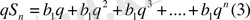ІУ. Жаңа сабақ:
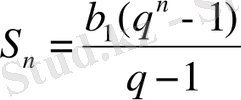
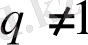
V. Есептер шығару.
Деңгейлік тапсырмалар
Геометриялық прогрессия берілген: 2; 6; 18 …
Оның сегізінші мүшесін табыңыз
«Ғажайып үштік»
Бүгінгі сабақтан алған әсерім
Оқушыларды бағалау.
Үйге тапсырма: №224
«Сиқырлы сөздер» ойыны
Мұғалім кез-келген өтінішті айтады, ал оқушы оны әдепті түрде айтуы керек.
Мысалы: Айнаш, дәптерді бер. «Айнаш, өтінемін дәптерді берші »
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz