Бір айнымалысы бар сызықтық теңдеу.. 6 сынып

Сыныбы: 6б
Сабақтың тақырыбы: Бір айнымалысы бар сызықтық теңдеу
Сабақтың мақсаты:
Білімділік: 1) түріндегі теңдеу - бір айнымалысы бар сызықтық теідеу
екенін үйрету;
2) бір айнымалысы бар сызықтық теідеуді шешіп, түбірін табу
дағдысын қалыптастыру;
3) құрамында теріс және оң бөлшектері бар санды өрнектердің
мәнін таба білуге үйрету;
Дамытушылық: математикалық сауаттылығын және жан-жақты логикалық
ойлау қабілетін дамыту:
Тәрбиелік: салыстырмалы танып білу, ұжымдық сезімін ояту, білім алудағы
бәсекелестікке баулу;
Сабақтың түрі: жаңа білім беру;
Сабақтың әдісі: сұрақ - жауап, түсіндіру, талдау, есептер шығару;
Көрнекіліктер: оқулық, интерактивті тақта, семантикалық кестерлер, бағалау
парағы
Пәнаралық байланыс: алгебра, информатика;
Жаңа технологиялық бағыт: интерактивті әдіс, Ж. Қараевтың <<Деңгейлеп оқыту>>
технологиясы

Сабақтың барысы:
* Ұйымдастыру бөлімі:
-амандасу;
-түгелдеу;
Үй жұмысын тексеру.
№ 799. (семантикалық карта арқылы)
өрнегінің мәнін тап:

е
е
т
у
д
Ң
;
1
14
-12
4
30
5
;
-6
26
13
24
19
23
;
11
3
25
6
27
8
;
10
15
7
29
-20
17
;
2
4,4
16
20
12
22
;
9
21
8
16
28
18

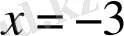
Жауабы: теңдеу.
* <<Кім зерек?>> зияткерлік ойыны:
( өткен тақырыпқа байланысты есептер)
*
*
*
*
* -4,8
* -2,7
* Жаңа сабақ.
теңдеуінде х - айнымалы (белгісіз). - теңдеудің сол жағы, теңдеудің оң жағы. Мұндай теңдеулер түрінде келтіріледі, мұндағы а - айнымалының коэффиценті, b - бос мүше.
түріндегі теңдеуді бір айнымалысы бар сызықтық теңдеу деп аталады.
Ықшамдау барысында теңдеу мәндес теңдеуге түрленеді. Мысалы,
теңдеуі мен теңдеуі мәндес теңдеулер.
Түбірлері бірдей теңдеулер мәндес теңдеулер деп аталады.
Теңдеулерді түрлендіріп, түріне келтіру үшін теңдеулердің мынадай қасиеттері пайдаланылады:
1-қасиет: теңдеудегі қосылғыштың таңбасын қарама-қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түленеді.
Теңдеудегі мұндай түрлендіруді енгізген ІХ ғасырдағы Орта Азия ғалымы- Мұхаммед бен Мұса әл-Харезми.
2-қасиет: теңдеудің екі жағын да нөлден өзге бірдей санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді.
1-мысал:

Бір айнымалысы бар сызықтық теңдеуді шешу үшін:
* Теңдеудің анықталу аймағы өзгермейтіндей етіп, оның бір жақ бөлігін де теңбе-тең түрлендіріп ықшамдау керек;
* Айнымалысы бар мүшелерді теңдеудің сол жағына жинақтау керек;
* Теңдеудегі ұқсас мүшелерді біріктіріп, теңдеудегі түріне келтіру керек;
* Теңдеудің екі жақ бөлігін де айнымалының коэффицентіне бөліп, теңдеудің түбірін табу керек.
теңдеуін шешудің үш жағдайы бар:
І. болса, теңдеудің екі жағын да а-ға бөліп, теңдігін жазамыз. Демек бұл жағдайда теңдеудің бір ғана түбірі болады.
2-мысал:
ІІ. болса, теңдеу теңдігі тің ешқандай мәнінде тура болмайды. Мұндай жағдайда теңдеудің түбірі болмайды.
3-мысал:
Жауабы: түбірі жоқ
ІІІ. болса, теңдеу түрінде жазылады. Кез келген санның нөлге көбейтіндісі нөлге тең болғандықтан , -тің кез келген мәнінде теңдік тура болады. Демек, теңдеуінің түбірі кез келген болады. Теңдеудің шексіз көп түбірі бар.
4-мысал:
Кез келген сан теңдеудің түбірі болады.
Есеп: Тең қабырғалы үшбұрыштың қабырғасы квадраттың қабырғасынан 2см кем. Квадраттың периметрі тең қабырғалы үшбұрыштың периметрінен 13см артық. Квадраттың қабырғасы неше сантиметр?
Шешуі: см - квадраттың қабырғасы, онда см - тең қабырғалы үшбұрыштың қабырғасы.

Тексеру:

* Есептер шығару
№835-837

* <<Кім жылдам?>>
(өткен тақырыпқа байланысты деңгейлік тапсырмалар)





* Жаңа сабақты бекіту сұрақтары:
* Бір айнымалысы бар сызықтық теңдеу дегеніміз не?
* Теңдеудегі а, b, х ті не деп атаймыз?
* теңдеудің шешудің жағдайларын атаңыз?
* Қорытынды.
Үйге тапсырма: №838
Оқушыларды бағалау