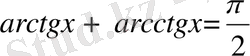Кері тригонометриялық теңдеу, теңсіздіктер

Сабақтың тақырыбы: Кері тригонометриялық теңдеу, теңсіздіктер

Сабақтың мақсаты:
1. Дидактикалық: кері тригонометриялық теңдеу, теңсіздіктерді шеше білуге үйрету
2. Тәрбиелік: ұқыптылыққа, жинақтылыққа, тапқырлыққа тәрбиелеу;
3. Дамытушы: оқушының ойлау қабілетін дамыту, ми жұмысының іскерлігін
арттыру.

Сабақтың түрі: практикалық.
Сабақты оқыту әдісі: ұжымдық, даралап оқыту.
Пәнаралық байланыс: оқушылардың білімін пәнаралық интеграциялау арқылы тиянақтау,
негізгі меже - функция қасиеттерін қолдануға бағыттау.

* Кіріспе мотивациялық бөлім
1.1. Проблемалық ахуал: кері тригонометриялық теңдеу, теңсіздіктерді шешудің дайын формуласы жоқ болғандықтан, оны формальды операциялар арқылы шешу мүмкін емес.
1.2. Сабақтың міндеті: осы проблемалық ахуалдан шығу жолдарын іздестіру: кері тригонометриялық функциялардың қасиеттерін қолдану арқылы қарапайым теңдеу, теңсіздіктерге көшу жолдарын меңгеру.
1.3. Бағытталған негіздегі іс- әрекеттер: теориялық материалды қайталап, есеп шығарудың негізін қалау.
1.4. Өткен тақырыптың өзектілігі: кері тригонометриялық функциялардың қасиеттерін білу оқушыларды есеп шығару әрекетіне дайындайды.

2. Танымдық жұмыстар
2.1. Оқушыларды қажетті ақпаратпен қамтамасыз ету: оқу материалдарын алдын ала
үлестіру.
2.2. Қосымша әдебиет қолдану:
1) Н.Я.Виленкин и др. Алгебра и начало анализа 10
2) М.Л.Галицкий и др. Углубленное изучение курса алгебры и математического анализа
2.3. Деңгейлік есептер шығару
3. Бақылау, бағалау: өздік жұмыс есептерін шығару.
4. Үйге тапсырма беру: Тарату материалындағы есептерді шығару.
5. Сабақты қорытындылау.

Оқу материалының мазмұны:
Теңдеу, теңсіздіктерді шешкенде кері тригонометриялық функциялардың ерекше қасиеттерін есте сақтап, олардың орындалуын қадағалау керек.
1. .
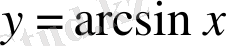немесе .
немесе . , тақ функция, өспелі функция.
2.
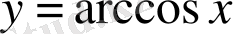
немесе .
немесе . . кемімелі функция.
3. .
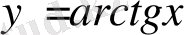, яғни .
, яғни . , тақ функция, өспелі функция.
4. .
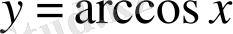, яғни .
, яғни . . кемімелі функция.
5.

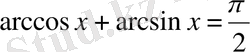
1. Алдымен қарапайым теңдеу, теңсіздіктерді қарастырайық.
1) , бұл екі бұрыштың теңдігі. Теңдіктің екі жағын синустаймыз:
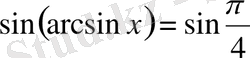
. Жауабы: .
2) , болғандықтан, .
3)
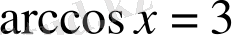
. Жауабы: .
4)

,
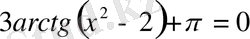
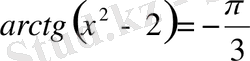
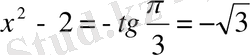
Жауабы: .
5) , өспелі функция.

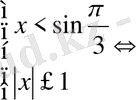
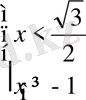
Жауабы: .
6)

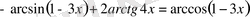
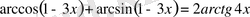
теңдігін пайдаланамыз:

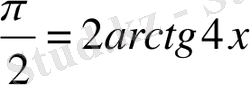
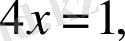
, . Жауабы: .
7) , болғандықтан.
Жауабы :.
8) , болғандықтан, .
Жауабы:
9)
.
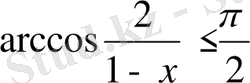
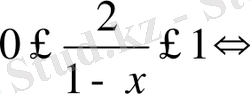
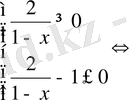
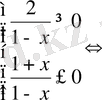
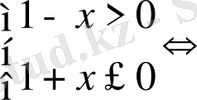
Жауабы:
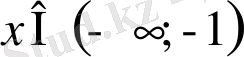
10)
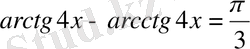
қасиетін қолданамыз.

.
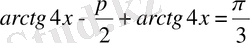
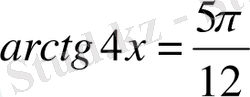
Жауабы: .
11)
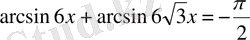
, келтіру формуласын қолданамыз.

,

, .
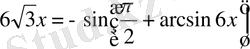
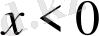
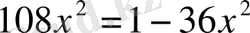
Жауабы: .

Жаттығулар:
Теңдеуді шешу:
*
*
*
*
*
*
*
*
*
*
*
*

Теңсіздікті шеш:

*
*
*
*
*
*
*
*
*
*
*
*

Екі жағында бірдей кері тригонометриялық функция болатын теңдеу, теңсіздіктер.
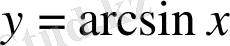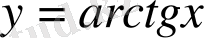, функцияларының өспелі, ал 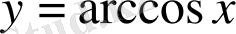, 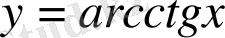функциялары кемімелі, 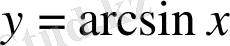, 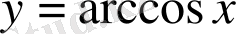функцияларының анықталу облысы 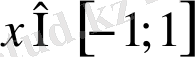болатынын қолдану керек.
Кері тригонометриялық функцияларға байланысты теңдеу, теңсіздіктерді қарапайым мәндес теңдеу, теңсіздіктермен алмастыру жолдарын қарастырайық.
*
*
*
*
*
*
*
*

Мысалдар:
* теңдеуін шешу керек. Ол үшін мәндес жүйеге көшеміз:

Жүйедегі теңдеуді шешеміз:

.
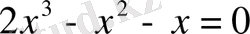
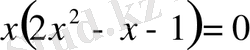
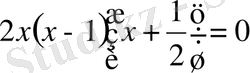
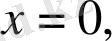
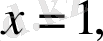
Мұндағы мәні жүйедегі теңсіздікті қанағаттандырмайды.
Жауабы: .
* теңдеуі теңдеуімен мәндес.

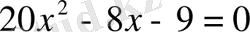
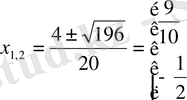
Жауабы: .
* теңсіздігін шешу үшін мәндес жүйеге көшеміз:

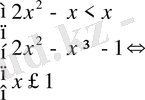
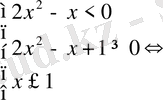
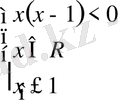
Жауабы:
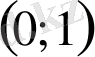
* теңсіздігін мәндес жүйемен алмастырамыз:

* теңсіздігін шешу үшін
теңсіздігіне көшеміз.
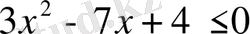
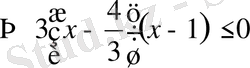
Жауабы :.

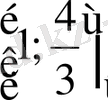Жаттығулар:
Теңдеуді шеш:
1)
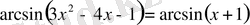
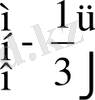
2)
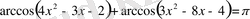
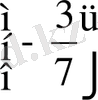
3)
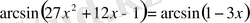
4)
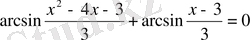
5)
*
*
*
*
*

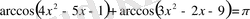
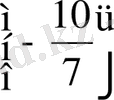
Теңсіздікті шеш:
*
*
*
*
*
*
*
*
*
*
*
*
3. Екі жағы да әртүрлі кері тригонометриялық функциялар болатын теңдеу, теңсіздіктер
* Егер саны теңдеудің шешімі болсын. Сонда , деп алсақ, , . Бұдан . Яғни .
* формуласын қолдансақ, .
* формуласы бойынша .
* формуласы бойынша .
* формуласы бойынша, .
* формуласы бойынша, .
Ескерту:
* - 4) пунктеріндегі теңдеулердің шешімі , болатындай саны болу керек. Олай болмаса, теңдіктің оң және сол жағындағы мәндер жиыны қиылыспайды. Сонда
*
*
*
*
Мысал.
* теңдеуін шешу керек.
Шешуі:

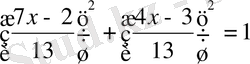
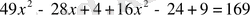
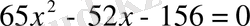
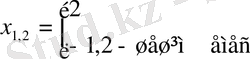
Жауабы: 2.
*

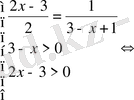
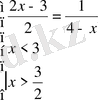
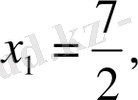
Жүйедегі теңдеудің шешімі . Олардың біріншісі шешім бола алмайды.
Жауабы :2.
* теңсіздігі сол жақтағы өрнектің мағынасы болатындай барлық х тер үшін дұрыс болады, себебі . Сондықтан
* Жауабы:

Жаттығу:
Теңдеуді шеш:
*
*
*
*
*
*

Теңдікті шеш:

*
*
*
*
*
*

4. Жаңа айнымалы енгізу әдісі:

Кері тригонометриялық функциялар енетін кейбір теңдеу, теңсіздіктерді жаңа айнымалы енгізу арқылы алгебралық түрге келтіруге болады. Сонымен қатар кері тригонометриялық функциялардың шектеулі екенін ескеріп отыру керек.

Мысалы:
*
болсын

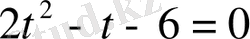
, болғандықтан, , .
Жауабы: .
*
болсын, мұндағы
,

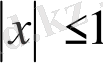
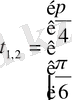
Сонда

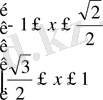
Жауабы:

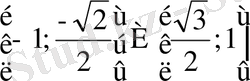
Жаттығу.

Теңдеуді шеш:
*
*
*
*
*
*

3. Бақылау: өздік жұмыс есептерін шығару, бағалау

4. Үйге тапсырма беру: Тарату материалындағы есептер.

5. Сабақты қорытындылау.