ҰБТ-дағы арифметикалық және геометриялық прогрессия есептерін тиімді шешу әдістері


ҰБТ кезіндегі прогрессия есептері және оны шығару жолдары
Шығыс Қазақстан облысы. Өскемен қаласы. “ Көпбейінді №3 мектеп-гимназиясы”
Математика пәні мұғалімі Маубакимова Айнұр Төлеуханқызы
Бүгінде мектеп қабырғасындағы жасөспірім-ертеңгі ел азаматы. Сол жастардың білімін саралап, келешекке жолдама беретін- Ұлттық бірыңғай тестілеу жүйесі.
ҰБТ кезінде кездесетін күрделі прогрессиялық есептердің, көпшілігі оқушыларға қиындық туғызады. Сондықтан ҰБТ кезіндегі күрделі прогрессия есептерін тиімді жолмен шығарудың жолдарын анықтау, ұсыну қазіргі мектептегі шешімін таба алмаған, өзекті мәселелердің бірі.
Арифметикалық және геометриялық прогрессия есептері алгебра бағдарламасында 9 сыныпта өтіледі. Бағдарлама бойынша тізбектер туралы алғашқы мәліметтер, сипаттамасы, арифметикалық, геометриялық прогрессиялардың анықтамалары және n мүшесінің формулалары беріледі. Оқулықта берілген есептер формулалар арқылы алгоритм бойынша шешу жолдарын қарастырады. Ал арифметикалық, геометриялық прогрессиялар қасиеттері арқылы теңдеу және теңдеулер жүйесін құра отырып шығару жолы ұсынылмайды. ҰБТ-де осы тақырыпқа берілген есептердің ішінде осы тәсіл арқылы шығарылатын есептер кездеседі. Ендеше түлектерге оларды шешудің тиімді жолдарын үйрету қажеттілігі туындайды.
Прогрессияға берілген есептерді шешудің тиімді жолдарының әдістемесі.
Ұлттық тестілеу орталығы дайындаған оқу- әдістемелік құралдардағы прогрессияға берілген есептерді зерделей келе, ҰБТ кезінде кездесетін есептерді төмендегіше жіктеуге болады:
1. Мазмұны бойынша:
- Белгісіз мүшесін немесе айырмасын (еселігін) табуға берілген есептер;
- Алғашқы n мүшесінің қосындысын табуға берілген есептер;
- Прогрессияның мүшелерінің санын табуға берілген есептер;
- Арифметикалық және геометриялық прогрессияға келтірілетін есептер.
2. Шығару әдісі бойынша:
- Теңдеу құру арқылы шығарылатын есептер;
- Теңдеулер жүйесін құру арқылы шығарылатын есептер.
Ендігі кезекте осы прогрессия есептеріне жеке-жеке тоқталып, оқушылардың шығару тәсілін талдап көрейік.
а) Мазмұны бойынша:
1. Белгісіз мүшесін немесе айырмасын ( еселігін) табуға берілген есептер:
1 Есеп. Егер
Шешуі: Бұл тізбек
Жауабы : 6
2 Есеп. Арифметикалық прогрессияның тоғызыншы мүшесін екінші мүшесіне бөлгендегі бөліндісі 5, ал он үшінші мүшесін алтыншы мүшесіне бөлгенде бөліндісі 2 болады да 5 қалдық қалады. Прогрессияның бірінші мүшесін және айырмасын табыңдар.
Шешуі:
Осыдан
Жауабы:
2. Алғашқы n мүшесінің қосындысын табуға берілген есептер:
3 Есеп. Шексіз кемімелі геометриялық прогрессияның қосындысы 26 және
Шешуі:
4 Есеп.
Шешуі:
 Жауабы:
Жауабы:
5 Есеп. Егер
Шешуі:
 мүшесінің қосындысының формуласы арқылы табамыз:
мүшесінің қосындысының формуласы арқылы табамыз:
3. Прогрессияның мүшелерінің санын табуға берілген есептер:
6 Есеп. -2, 7 саны бірінші мүшесі 2, 7-ге тең, ал айырмасы -0, 3-ке тең болатын арифметикалық прогрессияның мүшесі болады. Оның нөмірін табыңыз.
Шешуі:
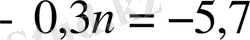 ;
;
7 Есеп.
Шешуі:
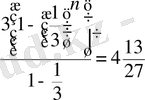 ;
;
Жауабы: n=5
4. Арифметикалық және геометриялық прогрессияға келтірілетін есептер:
8 Есеп. Үш сан геометриялық прогрессияны құрайды. Егер екінші саңды 2-ге арттырсақ, онда арифметикалық прогрессия болады, ал екінші тізбектегі үшінші саңды 9-ға арттырсақ, онда геометриялық прогрессия құрайды. Осы сандарды табыңдар.
Шешуі:
Ізделінді санды a, b, c деп белгілесек, есептің шарты бойынша.
a, b, c (Геометриялық прогрессия)
a, b+2, c (Арифметикалық прогрессия)
a, b, c+9 (Геометриялық прогрессия)
Осыдан
Табылған a және c-ның мәндеріне жүйенің екінші теңдеуіне қойсақ,
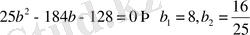
Жауабы:
Шығару әдісі бойынша:
1. Теңдеу құру арқылы шығарылатын есептер
9 Есеп . Теңдеуді шешіңіз
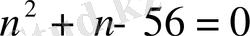 ;
;
2. Теңдеулер жүйесін құру арқылы шығарылатын есептер.
10 Есеп. Үш мүшесінің көбейтіндісі 64, ал олардың арифметикалық ортасы-
Шешуі: Есептің шарты бойынша:
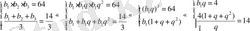
Осыдан
Жауабы: 1) 2; 4; 8; 2) 8; 4; 2.
Көріп отырғанымыздай мектеп оқушылары есептерді қосу, алмастыру, теңдіктің негізгі қасиетін қолдану тәсілі арқылы шығарды. Сонымен қатар бұл есептерді уақытты үнемдей отырып шығару жолдары да бар. Яғни, арифметикалық және геометриялық прогрессияның қасиеттерін қолдана отырып шығару алдыңғы тәсілден де тиімдірек болып келеді. Аталмыш тәсіл соңғы 3 жылда жиі қолданылып келеді. Бұл тәсілді қолдану жолдары ҰБТ-ға математика пәнінен дайындық кітапшаларында, әдістемелік құралдарда ұсынылып келеді. Атап айтсақ Ұ. Б. Жанасбаева, К. Б. Жанасбаевтың «ҰБТ. Математика» атты Алматы қаласынан 2010 жылы жарық көрген оқу әдістемелік құралында қасиеттері мен формулалары ұсынылып, мысалдар келтірілген. Бұл тәсілді қолдану жолы төмендегідей:
Арифметикалық прогрессияның қасиеттері:
1.
2.
3. Егер
4. Егер
5.
1 Есеп.
Шешуі: Жоғарыдағы 4 қасиет бойынша
2 Есеп.
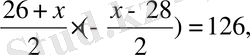
Жауабы: 16; -14
3 Есеп. Екі арифметикалық прогрессия берілген. Бірінші прогрессияның бірінші және бесінші мүшелер сәйкесінше 7 және 5-ке тең. Ал, екінші прогрессияның бірінші мүшесі 0, соңғы мүшесі
Шешуі: Есеп шарты бойынша
Прогрессияның айырымын табайық. Жалпы мүшенің формуласын қолданамыз.
5 -ші қасиет бойынша
4 Есеп.
Шешуі:
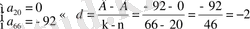
Жауабы:
5 Есеп. 2+4+6 . . . 2х=56;
Шешуі:
5 қасиетті пайдаланып,
Жауабы:
Арифметикалық прогрессия, оның қасиеттері мен ерекшеліктерін ескере отырып, тиімді формулаларға салып бірнеше есептер көрсетілді. Есептерді осы формулаларға қойып шығарған тиімді, себебі уақытты үнемдеуге мүмкіндік аламыз.
Геометриялық прогрессияның қасиеттері:
1.
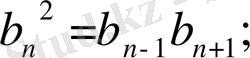
2.
3. Егер
4. Егер
6 Есеп.
Шешуі: 4 қасиетті қолдансақ,
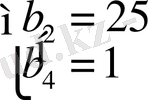 ,
,
Жауабы:
7 Есеп. Егер
Шешуі:
Жауабы:

Геометриялық прогрессияның негізгі формулалары және қасиеттеріне тоқтала отырып, оларды шығарудың тиімді жолдарын анықтауға тырыстым. Бұл есептерді шығаруда геометриялық прогрессия қасиеттерін басшылыққа алып есептерді шығарсақ, біріншіден, оқушыларға оңай, екіншіден, уақытты үнемдейміз.
ҰБТ кезінде кездесетін прогрессия есептерін шығару жолдарын төмендегідей салыстырмалы түрде тұжырымдауға болады:
9 сынып бағдарламасы бойынша оқушыларға таныс;
бұл тәсілдерді қолданып есеп шығаруға мүлдем аз тақырып бөлінеді, сондықтан меңгеру қиынға түседі;
бұл тәсілдерді қолдану үшін ең алдымен теңдеулер жүйесінің тәсілін жақсы меңгеру қажет;
теңдеулер жүйесінің тәсілдері тақырыбы үлкен бір ауқымды тақырып;
оны меңгере алмаған бала прогрессия есептерін шығаруда қиналады
бұл тәсілдерді ҰБТ кезінде қолдану тиімсіз, өйткені көп уақытты талап етеді
есептерді шығаруға 5-10 минут қажет.
Уақытты, ойлауды көп қажет ететіндіктен, математика пәнінен білім сапасының көрсеткішін төмендетеді.
Бағдарламаға енбеген, оқушыларға таныс емес тәсіл;
мектеп бағдарламысы бойынша оқытылмағанымен есепті шешу формуласы меңгеруге жеңіл;
теңдеулер жүйесінің тәсілін жақсы меңгеру қажеттілігі жоқ
бұл тәсілдерді ҰБТ кезінде қолдану тиімді, өткені уақыт үнемделеді;
есептерді шығаруға 1-2 минут қана уақыт қажет;
математика пәнінен жақсы білім сапасын көрсете алуға мүмкіндік туындайды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz