Логарифмдік функция және оның қасиеттері тақырыбына есептер шығару

Қарағанды облысы, Сәтбаев қаласы
«№7 жалпы орта білім беретін мектебі» КММ
Математика пәнінің І санатты мұғалімі
Турсынова Орниса Турсыновна

Сабақтың тақырыбы: Логарифмдік функция және оның қасиеттері
тақырыбына есептер шығару
Сабақтың мақсаты:
Білімділік:. Логарифмдік функция және оның қасиеттерін қорытындылау,
есептер шығаруда логарифмнің анықтамасы мен қасиеттерін қолдана білу
дағдыларын бекіту.
Дамытушылық: Теориялық білімдерін практикада ұштастыра отырып,ойлау және
есте сақтау, танымдық қабілеттерін дамыту.
Тәрбиелік: Оқушылардың белсенділігін арттыру,өз бетінше оқып, ізденуге,
шығармашылық қабілетін дамытуға, уақытты ұтымды пайдалануға тәрбиелеу.
Сабақтың түрі: Кіріктірілген сабақ (информатика және қазақ тілі)
Типі: білімді бекіту сабағы.
Методикалық әдіс-тәсілдер: Практикалық сабақ..
Сабақтың көрнекілігі: компьютер, интерактивті тақта, слайд, сөз жұмбақ
деңгейлік тест тапсырмалары,

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа дайындығын қадағалау.
ІІ. Үй тапсырмасын тексеру № 258, №359
№258
|а |ә |б |в |г |ғ |
|1 |(1; ∞) |0<х<1 |1/2 |0<х<1 |(1; ∞) |

№ 359
|а |ә |б |в |
|0<х<5 |(5 ; ∞) |([pic] ;|0 < х |
| | |∞) |<[pic] |

1. «Ой толғау». Өткен тақырыпты еске түсіру сұрақтары:
1) Қандай функцияны логарифмдік функция деп айтады ?

2) Неліктен теріс санның логарифмі анықталмайды ?
3) Қандай логарифм ондық логарифм деп аталады?
5) Натурал логарифм дегеніміз не?
6) Логарифмдік функцияның қасиеттерін ата.
Сабақтың жоспары:
1) Іздеген жетер мұратқа
2) Лездік тапсырма (Ауызша тапсырмалар)
3) Алғыр кілті (деңгейлік тапсырма) Сениматикалық карта
4) Ақпараттық сәт

5) Жол жетпегенге, ой жетеді (Гүл жинау)

6) Білім кілті(Тест)

1) «Іздеген жетер мұратқа» (логикалық тапсырма)
Логарифмнің негізгі қасиеттерін сәйкестендіру арқылы қайталау
1. alogab 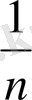[pic]log a b

2. loga a logax
+logay
3. loga1 p loga x

4. [pic] logax
5. loga (xy) . 0
6. loga(x/y) log a b

7. loga xp [pic]log a
b
9. log 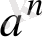[pic]b loga x –
loga у
10. log a[pic] bn 1
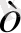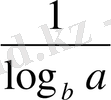11. [pic] b

2) «Лездік тапсырма» (ауызша есептер)
log2 64 = 6 log0,4 0,16= 2
log40 1600 = 2 log6 216= 3
log4 х= 4 , log5 х= 3
x = 256 x = 125
3 log3 81= 81 4 log16 7 = [pic]

lg10=1 3 log3 3+2 = 3 log3 3 ∙3 2 =
9∙3 = 27
logx 16 =4 logx 25= 2
x = 2 x = 5

3) «Алғыр кілт»і (деңгейлік тапсырма) 3 қатар жеке сениматикалық картаны
толтырғанда берілген нақыл сөздердің авторлары шығады
1 қатар.
«Мен теорияның өте қызық дәлелдеуін таптым, бірақ орын жоқтықтан жаза
алмай отырмын» Кімнің сөзі? (Пьер Ферма)
[pic]

| |Жауаптары |
|Тапсырма |4,86 |1 |3 |5 |0|logx625= 4 |Д |В |С |Ф |А |
| 9x мәнін х = log3 9 +[pic]1,5 |Т |Л |Е |К |И |
|log3 [pic] есептеңіз | | | | | |
|log10 x= 0 |Й |Р |Қ |Н |О |
|log2x < 4 |П |Э |Б |Ғ |М |
|log4x = 1/3log4216 – 2 log410 + 4 |А |Ә |Е |Г |Ц |
|log4 3 | | | | | |

Ферма Пьер - француз  математигі, физигі. Мамандығы бойынша заңгер. 
Сандар теориясының негізін қалаушылардың бірі. Осы теорияның бір теоремасы
Ферманың есімінен аталады (қ. Ферма теоремасы). Ферма геометриядағы
координаттар тәсілін Р.Декарттан бұрынырақ жүйелі түрде дамытқан. Ғалым
шексіз аз шамаларды есептеуде дифференциялаудың жалпы заңын ашты. Ол
максимум мен минимумды  (экстремумдарды)  табатын есептермен, қисықтарға
жанама жүргізу тәсілімен, дененің ауырлық центрін анықтаумен,
қисық(шеңбер) доғасының ұзындыған есептеумен, ықтималдық теориясының
есептерін шешумен, т.б. шұғылданды. Ферма физикада Ферма принципі деп
аталатын геометриялық оптиканың негізгі принципін тұжырымдады.

Шешуі:
1) logx625= 4 х4 = 625 x= 5
2) 9x мәнін х = log3 9 +[pic]1,5 log3 [pic]
х = log3 9 +[pic]1,5 log3 [pic]
x = 2 +[pic]5 [pic](-1 ) = 0,5 9х = 90,5 = 3
3) log10 x= 0 х = 1
4) log2 x < 4 х< 16 Ж ауабы: 0< х < 16

5) log4x = [pic] log4216 – 2 log410 + 4 log4 3
log4x= log4( 63[pic]log410 2 + log4 3 4
log4 x = log4 [pic]
x = [pic]= [pic] = 4,86

2қатар
«Математика – барлық ғылымдардың тұңғышы және оларға пайдалы да, қажет
те». Кімнің сөзі (Роджер Бэкон).
[pic]

| |Жауаптары |
|Тапсырма |[pic] |[pic] |(9; ∞) |3 |4 |
|logх 64= 3 |А |Р |Л |И |Б |
|5x мәін x = log59 + [pic] |П |С |Т |Э |Ф |
|есепте | | | | | |
|log3x >2 |Й |Д |К |О |П |
|log1/2x= 1 |Ю |О |Р |С |Т |
|log3 x=2log96 – log912 |Н |А |Й |Г |О |

Роджер Бэкон — XIII ғасырдағы ағылшын философы және табиғат зерттеуші,
әрі астрономшы.
Бэкон философия ғылымының практикалық функциясына ерекше көңіл
бөледі. Оның ойынша философия ғылыми білімдердің көмегі арқылы адамға
табиғатты игеруге көмектесуі қажет деген қағиданың авторы . Ғылымдарды
да Бэкон адамға пайдалылығына байланысты классификациялайды.
Шешуі:

1) logx 64 = 3 x3 = 64, x 3 = 43 , x = 4

2) 5x мәін x = log59 + [pic]
х = log59+ log5 [pic]
х = log5 (9 [pic]) = = log53
5x = 5 log53 = 3 Жауабы: 3

3) log3x >2, x > 9, Жауабы: (9; ∞)
4) log1/2x= 1 х = [pic] Жауабы: [pic]
5) log3 x=2log96 – log912

log3 x =log962 – log912

log3 x = log936 – log912

log3 x = log9 [pic]

log3 x = log93

log3 x = log323 , log3 x = 1/2log3 3 , log3 x = ½
х = [pic]

3 қатар
«Математика ғылымдар патшасы, ал арифметика математика патшасы» Кімнің сөзі
(Карл Фридрих  Гаусс)
[pic]

| |Жауаптары |
|Тапсырма |25 |0< x<1 |27 |4 |6 |
|log 3 x= 3 |А |В |Г |С |Т |
|10х мәін х = lg2 + [pic] |Н |К |О |Л |А |
|есепте | | | | | |
|logх 256 = 4 |0 |П |Р |У |С |
|log3x < 0 |Т |С |А |Ф |Ж |
|log5 x = 1/2log3144 + log30,75 |С |Т |Б |И |Н |

Карл Фридрих Гаусс — XIX ғасырдың ұлы неміс математигі, астрономы және
физигі. 1824жылы Санкт-Петербург ғылым академиясының құрметті мүшесі
болған. Оның еңбектері алгебраның, сандар теориясының, дифференциалдық
геометрияның, тартылыс теориясының, электр және магнит құбылыстарының
классикалық теориясының, теориялық астрономияның дамуына орасан зор ықпал
етті Гаусс сондай-ақ, астрономия, ықтималдықтар теориясы, шексіз қатарлар
теориясы, потенциалдар теориясы, т.б. салалар бойынша да іргелі еңбектер
жазған, Жоғары математиканың негізін қалаған.
Шешуі:

1) log3 x = 3 x = 27

2) 10х мәін х = lg2 + [pic]
x = lg2 + lg3 = lg6

10 x = 10 lg6 = 6

3) log3x < 0 , x < 1, 0< x < 1
4) logх 256 = 4 , x4 = 256, x4 = 44 , x = 4
5) log5 x = [pic] log3144 + log30,75
log5 x = log3(12)2[pic] + log30,75
log5 x = log3(12 ∙ 0,75)
log5 x = log39 log5 x = 2 x = 25
3,,
4) «Жол жетпегенге, ой жетеді» (Гүл жинау)

Балалар, енді мына құмыраға гүл шоқтарын тапсырмалар орындау
арқылы толтырайық. Ол үшін әрбір гүлдің тапсырмаларын орындай отырып,
гүлдің ашылып жайқалуына көмектесейік. Сонымен қатар біздер мына
тапсырмадағы жауапты тақтаға жазып кетеміз.

Сөз жұмбақ шешу. Логарифмнің қысқаша шығу тарихын айту.
1) Бүтін оң сандар қалай аталады. (натурал)
2) Үшбұрышқа неше диогналь жүргізуге болады? (ноль)
3) Туынды терминін енгізген кім? (Лагранж)
4) Ғылым патшасы (математика)
5) Барлық кабырғалары тең төртбұрыш (квадрат)
6) Тәуелсіз айнымалы қалай аталады? (икс)
7) математикалық сан және қарапайым амалдарды оқитын бөлім (арифметика)
8) 106 –ші қалай оқылады? (миллион)

1

2

3

4

5

6

7

8

Балалар сөз жұмбақ шештік .Сонда бізде қандай сөз шықты? Міне, енді.
мына құмыраға жайқалған гүл шоқтарын да жинадық. Сендерге рахмет. Осындай
гүлдей жайнап жүре беріңдер.
Балалар міне сөз жұмбақ шештік . Сонда бізде қандай сөз шықты? (Логарифм)
Енді мына құмыраға жайқалған гүл шоқтарын да жинадық. Сендерге рахмет.
Осындай гүлдей жайнап, жарқырап жүре беріңдер.

Логарифмнің қысқаша шығу тарихын айту

5) «Білім кілті» (активоидпен орындалатын тест тапсырмалар)

1-нұсқа.
1. Есептеңдер: [pic]
А) 9;
В) 18;
С) 3;
D) 0;
Е) 10.
2. Теңдеуді шешіңдер: [pic]
А) 4;
В) 1/2;
С) 0;
D) 1;
Е) 16.
3. Теңдеуді шешіңдер: log 2 х = 2
А) 4;
В) 2;
С) 3;
D) 1;
Е) 0.
4. Өрнектің мәнін тап: log2log2log4 16?
А) 2;
В) 4;
С) 1;
D) 8;
Е) 0.
5. Теңдеуді шешіңдер: log 3 243
А) 6;
В) 3;
С) 4;
D) 5;
Е) 2.
6. Есептеңдер: [pic]
А) 98;
В) 49;
С) 0;
D)24;
Е) 1.
7. Теңдеуді шешіңдер: [pic]
А) 5;
В) 6;
С) 0;
D) 1/2;
Е) 1.
8. х-тің мәнін табыңдар: log 9 х = 4
А) 46562;
В) 6561;
С) 6560;
D) 6566;
Е) 6570.
9. Өрнектің мәнін тап: log2log2log3 81?
А) 9;
В) 5;
С) 1;
D) 3;
Е) 0.
10. Есептеңдер : [pic]g 2[pic]log2[pic]

А) 4;
В) -4;
С) 2;
D) 3;
Е) 1

Тест жауабы:
|Тапсырмалар |
|1 |2 |3 |4 |5 |
|Мен білемін | | | | |
|Менің қолымнан| | | | |
|келеді | | | | |
|Менің үйренгім| | | | |
|келеді | | | | |

-----------------------
т

е

м

н

ь

а

Л

р

О

н

Л

а

р

у

т

а

на

л

Л

Г

а

ж

А

а

а

а

к

и

т

а

м

Р

т

а

к

в

с

И

к

м

е

а

к

т

и

а

Ф

р

и

л

н

о

и

л

МИ

и